Vortrag_GdW_2019-11-28
Dieser Text: Kurzvortrag "Grundzüge der Datenanalyse" in der Vl GdW 2019-11-28
unüberwachtes vs. überwachtes Lernen
überwachtes Lernen: in den Beispielen ist vorgegeben, was erkannt werden soll; die Daten sind "gelabelt"
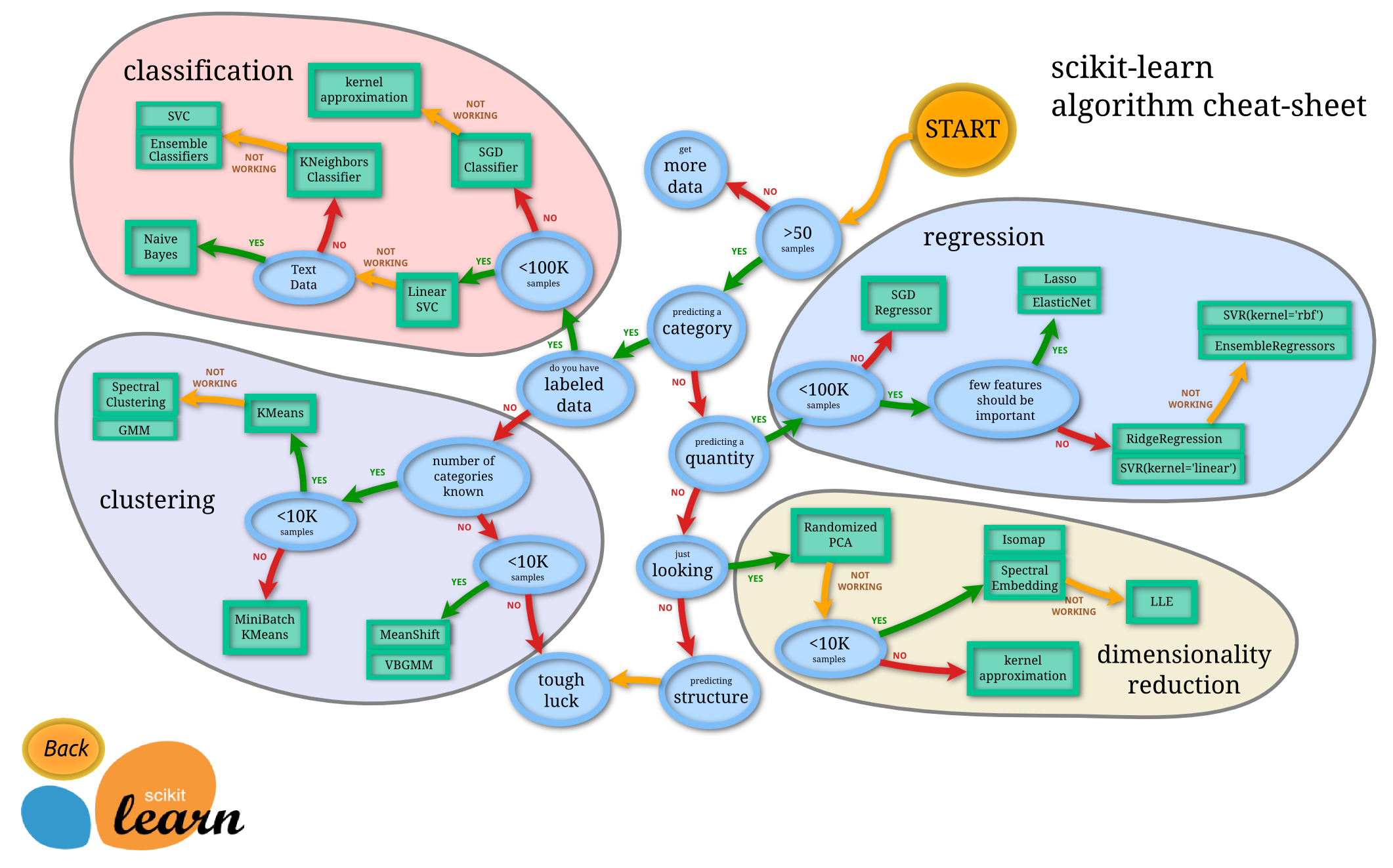
- Klassifikation: Es soll eine Klasse vorhergesagt, z.B. m/f, Weißwein/Rotwein, oder auf einem Foto ein Muffin von einem Chihuahua (Quelle ) unterschieden werden .. .Bsp. k-nearest-neighbour (KNN), logistische Regression (sic!)
- Regression: Es soll ein numerischer Wert vorergesagt werden, z.B. Gewicht, Überlebenswahrscheinlichkeit, Hauspreis
unüberwachtes Lernen: die Daten sind nicht "gelabelt"; in den Daten sollen Strukturen (z.B. Segmente) erkannt werden
- Clustering: der Algorithmus soll anhand von Beipielen aus einer (durch den Algorithmus vorgegebenen) Gruppe von möglichen Regelmäßigkeiten die naheliegenderen erkennen; Bsp: Clusteranalyse
- Dimensions-Reduktion: es sollen die "relevanten" Attribute eines Datensatzes gefunden werden; Bsp: PCA
Merke:
- Bei unüberwachtem Lernen ist die richtige Antwort (dem Algorithmus) gänzlich unbekannt,
- bei überwachtem Lernen ist die Antwort (in ausreichend vielen Beispielen) vorgegeben.
- falls die richtige Antwort numerisch ist: Regressions-Problem
- falls kategorial: Klassifikations-Problem
ausführliche Klassifikation von Problemtypen nach CRISP-DM: Data mining problem types nach CRISP-DM
Wir betrachten im folgenden nur überwachtes Lernen.
Ablauf von ML
Ablauf ganz grob:
- Training: Algorithmus "lernt" Vorhersage-Modell
- Prediction: Vorhersage-Modell "entscheidet"
sehr ausführlich: CRISP-DM phases, tasks, outputs
Schritt 1: Training
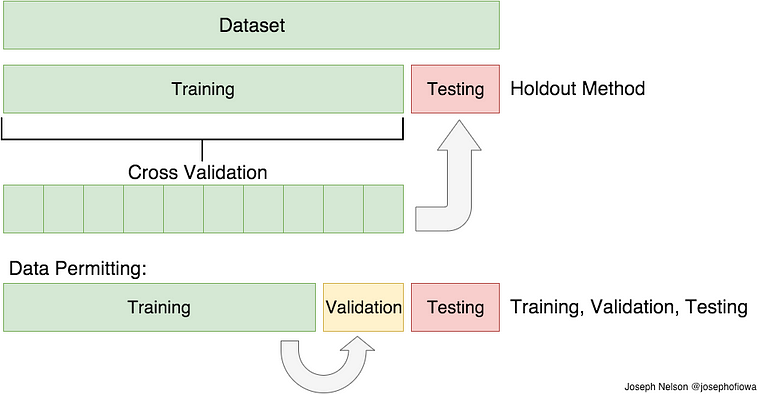
Schritt 0: Die verfügbaren Beispiele werden in ein Trainings- und ein Test-Set aufgeteilt. Das Test-Set wird weggeräumt - es wird im folgenden ausschließlich mit dem Trainings-Set weitergearbeitet!
Schritt 1a: Lernen des Vorhersage-Modells. Der Lern-Algorithmus wird mit dem Trainings-Set gefüttert. Als Ausgabe erzeugt der Lern-Algorithmus ein Vorhersage-Modell.
Der Lern-Algorithmus erzeugt also auf Grundlage von Beispielen einen Algorithmus, den man dann für Klassifikation oder Regression von neuen Beispielen einsetzen kann.
- Normalerweise ist der Lern-Algorithmus komplex, und die Erstellung des Vorhersage-Modells nimmt viel Expertenzeit und Rechner-Ressourcen in Anspruch.
- Dazu im Unterschied lässt sich das Vorhersage-Modell oft "deklarativ" als eine Menge von Parametern, Regeln oder mathematischen Formeln aufschreiben, mit denen man für neue Beispiele sehr schnell - bei manchen Anwendungen im Millisekunden-Rhythmus - neue Vorhersagen treffen kann.
Schritt 1b: Das Vorhersage-Modell bewerten. Dem Vorhersage-Modell zeigt man das im Schritt 0 abgespaltene Test-Set, bei dem die richtigen Antworten verborgen wurden. Das Modell sagt daraufhin für die Beispiele im Test-Set entsprechende Klassen oder numerische Werte voraus. Anhand der Abweichunungen von den vorhergesagten und den nun wieder offengelegten richtigen Antworten werden Gütemaße für das Vorhersage-Modell berechnet.
- Zur Erzeugung dieses Modells wird das Trainings-Set oft zyklisch in ein Trainings- und ein Validation-Set aufgeteilt (cross validation). Es wäre ein schwerer Fehler, in diesen Schritt Beispiele aus dem Test-Set hineinsickern zu lassen.
Bei dem in unserer Veranstaltung betrachteten Algorithmus "glmnet / elasticnet" werden in Schritt 1a zwei Tuning-Parameter (Stärke und Art einer sogenannten Regularisierung) in einem breiten Wertebereich variiert. Auf diese Weise werden systematisch hunderte Vorhersage-Modelle erzeugt und (z.B. mit cross-validation) getestet. Diejenige Kombination von Tuning-Parametern, die die besten Scores liefert, halten wir fest.
In Anschluss (!) an Schritt 1b lassen wir für die beste Kombination an Tuning-Parametern aus 1a den Lern-Algorithmus nocheinmal mit allen verfügbaren Train- und Test-Daten durchlaufen, um ein bestmögliches Modell deployen zu können.
Schritt 2: Prediction
Schritt 2: Einsatz des Vorhersage-Modells im Feld. Das Vorhersage-Modell sagt jetzt "autonom" Werte für bisher unbekannte Beispiele voraus. (Ein Lernen findet hier im allgemeinen nicht statt.)
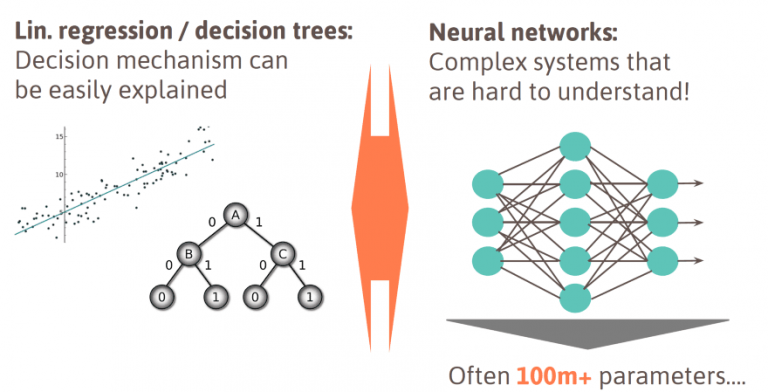
Einfach strukturierte Vorhersage-Modelle, die sich mit vernünftigem Aufwand vergleichsweise klar nachvollziehen oder durch eine Inspektion vergleichsweise informiert bewerten lassen, nennt man White Box Modelle.
Modelle, die zu komplex oder bauartbedingt überhaupt nicht nachvollziehbar sind, nennt man Black Box Modelle.
Bisweilen erfordern (z.B. Finanz-) Regularien oder ethische Randbedingungen gut erklärbare White Box Modelle - selbst dann, wenn solche typischerweise schlechtere Gütescores aufweisen nicht nachvollziehbare Black Box Modelle.
Gütekriterien von Regressionsmodellen
Regressionsmodelle sagen numerische Werte voraus, mit denen man rechnen kann. Insbesondere gibt es das Konzept "Abstand" zwischen Punkten im n-dimensionalen Raum.
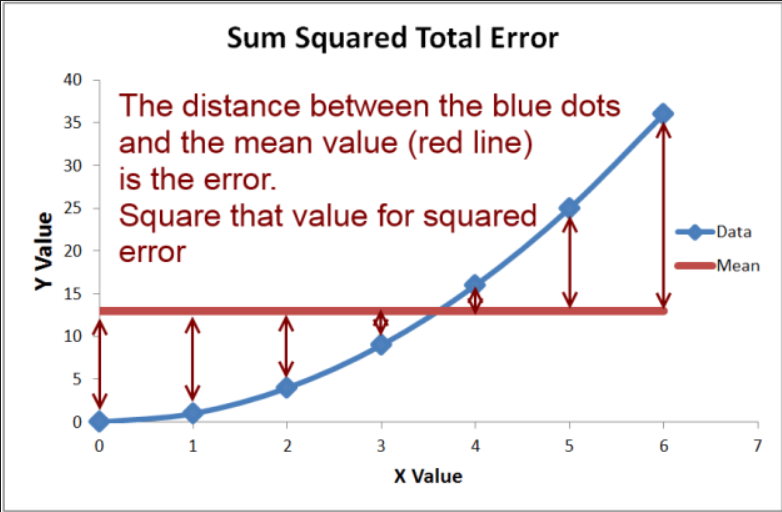
Die Güte eines Modells wird traditionell als Abstand zwischen Vorhersage und tatsächlichem Wert ausgedrückt, genauer:
- Euklidischer Abstand (L2-Norm): Wurzel der Summe der quadrierten Abweichungen, Mean Square Error (MSE)
- Manhattan-Abstand (L1-Norm): Summe der Beträge der Abweichungen, Mean Absolute Error (MAE)
In der mathematischen Grundlagenausbildung gehört das Ausrechnen einer möglichst genauen, d.h. den MSE optimal minimierenden Regressionsgerade zum Standrad-Lehrstoff. In der Praxis des ML gelten solche der reinen Lehre entsprechende Regressionsgeraden als Kunstfehler:
- "if you are using regression without regularization, you have to be very special!" https://www.analyticsvidhya.com/blog/2016/01/complete-tutorial-ridge-lasso-regression-python/
Der Grund liegt darin, dass rein mathematisch optimal angepasste Regressionsgeraden an Über-Anpassung leiden: Sie zeigen sehr gute scores bei bekannten Daten, die bei unbekannten Daten aber stark abfallen. Im Modell selbst erklärt sich solches Verhalten an einer hohen Varianz der beteiligten Parameter, die man durch regularisierte Modelle tendenziell zu vermeiden sucht.
Gütekriterien von Klassifikationsmodellen
Eine Klassifikationen zeichnet sich dadurch aus, dass man mit den Werten aus der Vorhersage nicht sinnvoll rechnen kann, und sie nicht einmal semantisch sinnvoll in eine Ordnung bringen (und daher höchstens beliebig auf natürliche Zahlen abbilden) kann. Wo man aber nicht sinnvoll von einem "Abstand" zwischen vorhergesagten und tatsächlichen Werten sprechen kann, versagen auch auch die Gütekriterien der Regressionsmodelle.
Als Vereinfachung für kategoriale Wertebereiche mit mehr als zwei Werten betrachtet oft zunächst Wertebereiche mit genau zwei unterschiedlichen Klassen, die man der Einfachkeit halber mit "0 / negativ" und "1 / positiv" bezeichnet. (Man kann sich hier z.B. einen Schwangerschaftstest vorstellen).
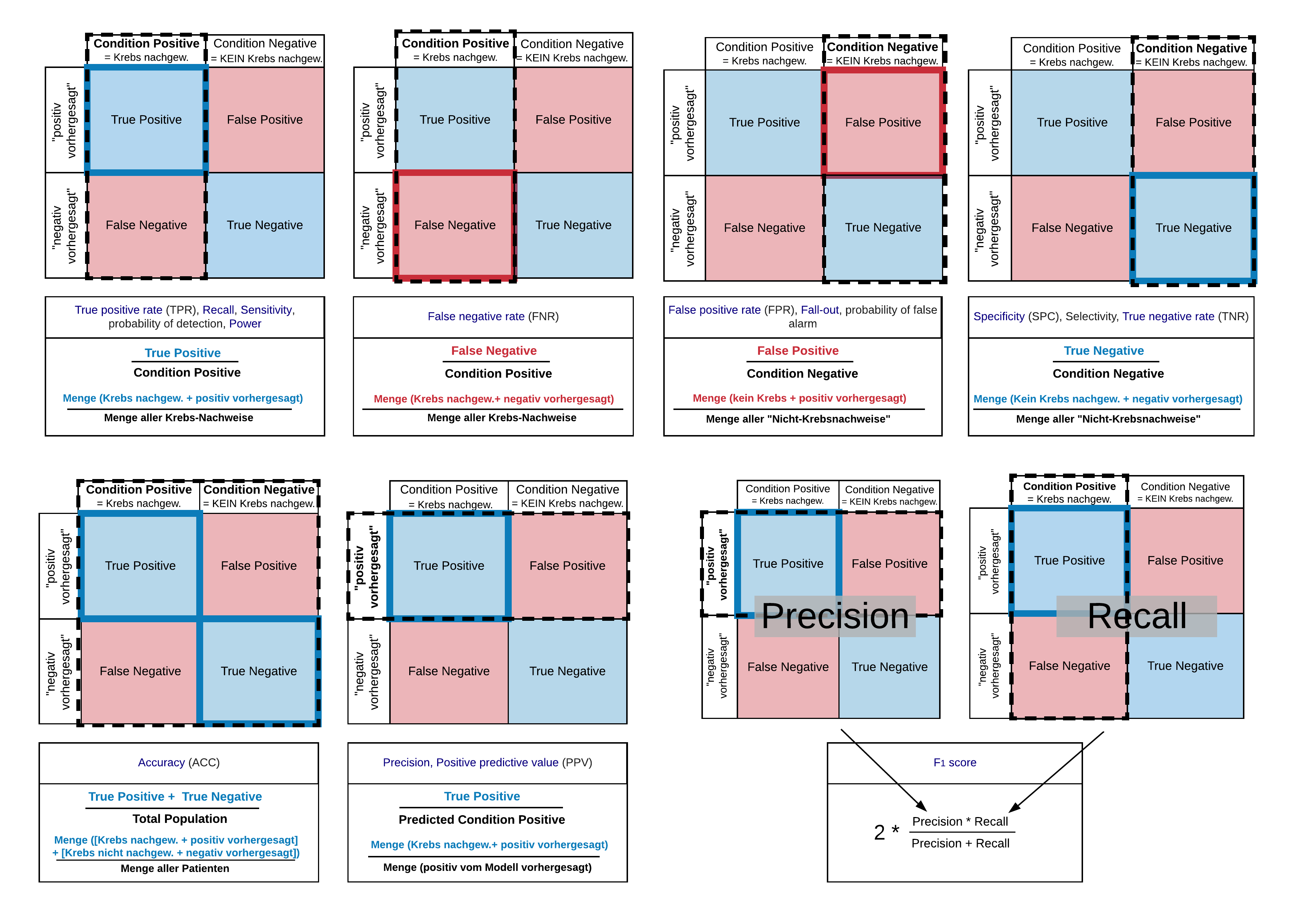
Gütekriterien von Klassifikationsmodellen basieren auf vier Basiswerten, die im Schritt 1b "Das Vorhersage-Modell bewerten" durch einfaches Auszählen bestimmt werden:
- TP: Eine positive Vorhersage stößt auf einen tatsächlich positiven Fall, d.h. die positive Diagnose "stimmt": true positive!
- FP: Eine fälschlicherweise positive Vorhersage stößt auf einen tatsächlich negativen Fall, d.h. die positive Diagnose stimmt *nicht*: false positive!
Die Begriffe TN und FN verstehen sich entsprechend:
- TN: Eine negative Vorhersage stößt auf einen tatsächlich negativen Fall, d.h. die negative Diagnose stimmt: true negative!
- FN: Eine fälschlicherweise negative Vorhersage stößt auf einen tatsächlich positiven Fall, d.h. die negative Diagnose stimmt *nicht*: false negative!
Viele Klassifikations-Modelle liefern intern nicht eine "0" oder "1", sondern eine Reelle Zahl im Intervall [0,1], wobei Abbildung auf "0/1" einfach durch einen Schwellwert bestimmt wird. Die Werte von TP, FP, TN, FN hängen natürlich sensibel von diesem Schwellwert ab:
- Ein eher hoher Schwellwert führt zu einem eher unempfindlichen Klassifikator, der nur dann ein TP auswirft, wenn die "1" vergleichsweise sicher ist - mit dem Nachteil, dass möglicherweise viele tatsächlich positive Fälle als FN klassifiziert werden.
- Ein eher niedrigen Schwellwert führt zu einem eher empfindlichen Klassifikator, der schon dann ein TP auswirft, wenn nur der Verdacht auf eine "1" besteht. Zwar werden jetzt alle positiven Fälle auch tatächlich als positiv erkannt - aber mit dem Nachteil, dass vermutlich auch viele tatsächlich negative Fälle als positiv klassifiziert werden.
- Wie aus den 4Werten {T|F}{P|N}, die ja auch noch durch einen Schwellwert parametrisiert sind, eine einzige aussagekräftige Kennzahl errechnet werden kann, siehe unten "AUC".
Die Wahl eines geeigneten Schwellwerts hängt u.A. von den monetären oder psychischen Kosten ab, die bei Falschklassifikationen (FP, FN) entstehen: Bei einem Self-Service-Schwangerschaftstest könnte man zu einem eher niedrigen Schwellwert tendieren und die Semantik von "1" als *möglicherweise* schwanger definieren. Das kann sinnvoll sein, wenn sich daraus weitere Vorsorgeuntersuchungen ergeben oder Schaden für den Embryo frühzeitig vermieden wird. Umgekehrt möchte man bei z.B. einem Krebstest vielleicht eher vermeiden, zu viele falsch positive Diagnosen zu stellen, und eher einen hohen Schwellwert ansetzen - auch aus dem Argument heraus, dass es ein Recht auf Unwissenheit gibt.
ROC und AUC
Die Güte eines Regressionsmodell lässt sich mit dem MSE, also einer einzigen Zahl angeben. Bei einem Klassifikator haben wir die vier Werte TP, FP, TN, FN, die zudem noch von der Wahl eines Schwellwerts abhängig sind. Auch hieraus lässt sich einzige aussagekräftige Zahl erzeugen.
Dazu untersucht man was passiert, wenn man den Schwellwert eines Klassifikators in kleinen Schritten von 1 auf 0 zurückfährt (und damit schrittweise seine Empfindlichkeit) erhöht. Bei einem zunächst hohem Schwellwert werden zunächst vorwiegend die eindeutig positiven Beispiele (TP) mit "1" klassifiziert. Man hat nur wenige FP, leider jedoch einige FN zu verzeichnen. Senkt man den Schwellwert, erfasst man auch die bisherigen fälschlicherweise als negativ klassifizierten Beispiele (FN) nun zutreffend als positiv (TP) - um den Preis, dass nun auch mehr und mehr tatsächlich negative Beispiele fälschlicherweise als positiv (FP) klassifiziert werden.
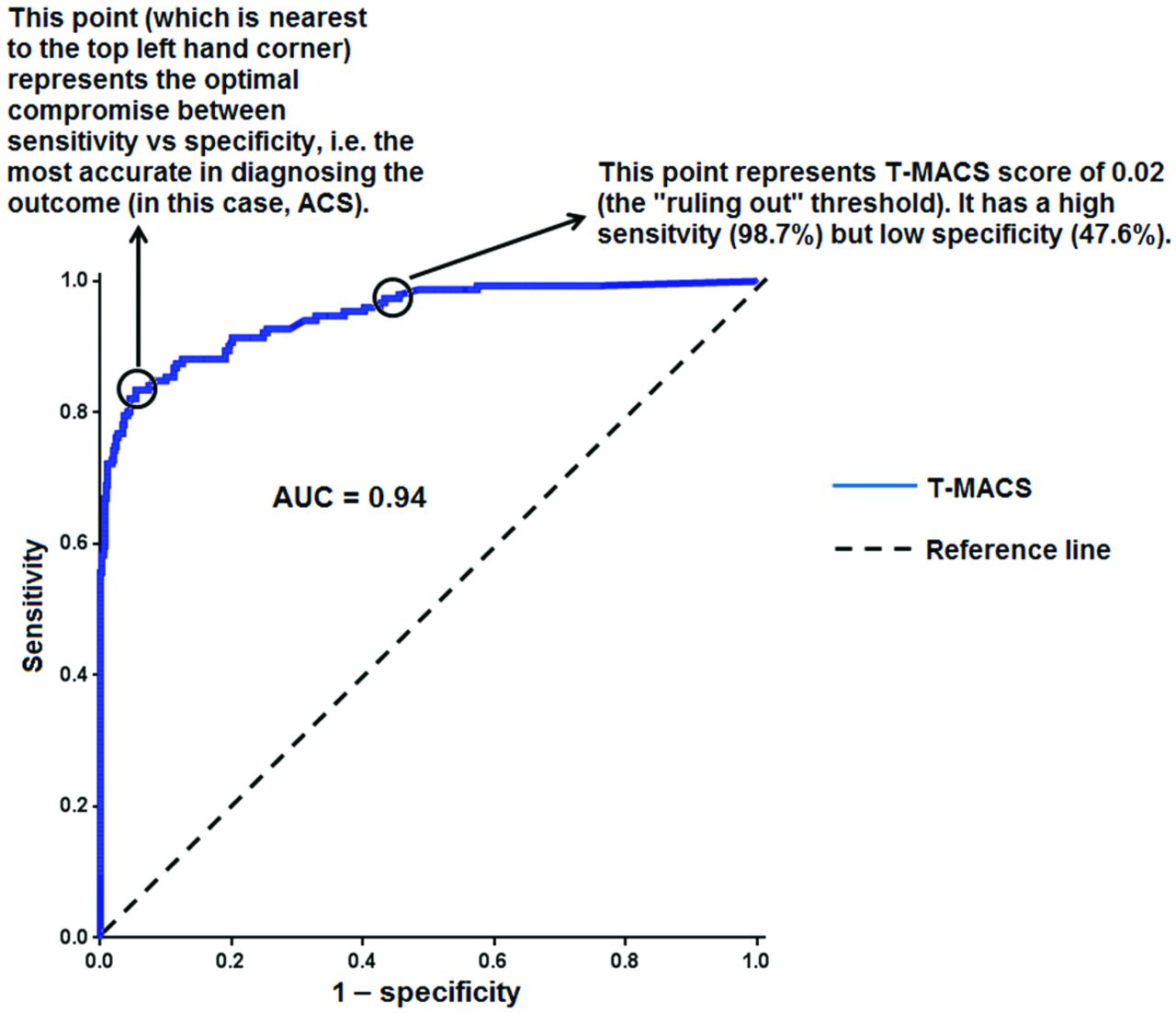
Bei obigem Vorgehen erhält man eine Tabelle mit 3 Spalten: Schwellwert, FN, TP. Bezeichnet man in einem Koordinatensystem die x-Achse als FP-Rate und die y-Achse als TP-Rate, lassen kann zu jedem Schwellwert aus dieser Tabelle der zugehörige FP (x-Achse) und TP (y-Achse) Wert im Koordinatensystem eintragen. (Achtung: Es wird also nicht der Schwellwert selbst eingetragen, sondern zu jedem Schwellwert der zugehörige Punkt (FP, TP)). Die Kurve, die man als Ergebnis dieses Vorgehens erhält, nennt man receiver operating characteristic (ROC) Kurve.
Bei einem guten Klassifikator steigt diese Kurve idealerweise steil an, um sich dann asymptotisch der Geraden y=1 zu nähern; die Kurve schmiegt sich also idealerweise an die obere linke Ecke an. Bei einem schlechten Klassifikator steigen TP und FN eher gleichmäßig an. Nähert sich unsere Kurve der Diagonalen, können wir statt unserem Klassifikator auch gleich Zufallszahlen würfeln. (Falls die Kurve unterhalb der Diagonalen bleibt und erst spät ansteigt, haben wir einen Vorzeichenfehler gemacht.)
Aus dieser Kurve lässt sich auch ein optimaler Schwellwert ablesen: Optimal ist der Schwellwert dann, wenn sich eine weitere Zunahme von TP nicht mehr lohnt, weil die zu viele FP hinzukommen. Dieser Punkt ist dort erreicht, wo die Kurve die gleiche Steigung hat wie die Diagonale (an die sie sich bei weiterem Absenken des Schwellwerts ja wieder annähert).
Wenn man - analog zum MAE oder MSE eines Regresisonsmodells - lediglich eine einzige Zahl sucht, um grob die Güte eines Klassifikators zu kennzeichnen, eignet sich die Fläche unter der ROC-Kurve ganz gut, genannt Area under curve (AUC). Bei einem idealen Klassifikator ist fast der gesamte Quadrant ausgefüllt, die AUC geht also gegen 1. Bei einer schlechten (im Extremfall zufälligen) Klassifikation nähert sich die ROC-Kurve der Diagonalen an, die AUC geht also gegen 0.5. (Und bei einer AUC < 0.5 schauen wir unseren Code nochmal ganz genau an, ok?)