Fairness (Bsp. “Jockey”)#

Dieses Notebook: Eine Rekonstruktion von Szenario 1 aus dem Blog-Beitrag von Astrid Schomäcker: Die mathematischen und ethischen Herausforderungen fairer KI ; wissenschafliche Grundlage: <https://arxiv.org/pdf/1610.07524.pdf)

  • codiert als Jupyter Notebook

  • incl. Erklärung in eigenen Worten JB

  • mit Bezug auf andere Aufsätze, die dieses Fallbeisiel diskutieren

  • mit dem Versuch einer neuen Visualisierung der Confusion Matrix

Originaltext (Auszug)

(Originaltext von Astrid Schomäcker. JB beansprucht keine eigene Werkleistung in Bezug auf den Inhalt.)

  • Wörtlicher Auszug aus: Dr. Astrid Schomäcker: Die mathematischen und ethischen Herausforderungen fairer KI: https://lamarr-institute.org/de/blog/ki-fairness/ (1. Dezember 2021)

  • JB: Wir glauben einen Zahlenfehler bemerkt zu haben und korrigieren diesen explizit.

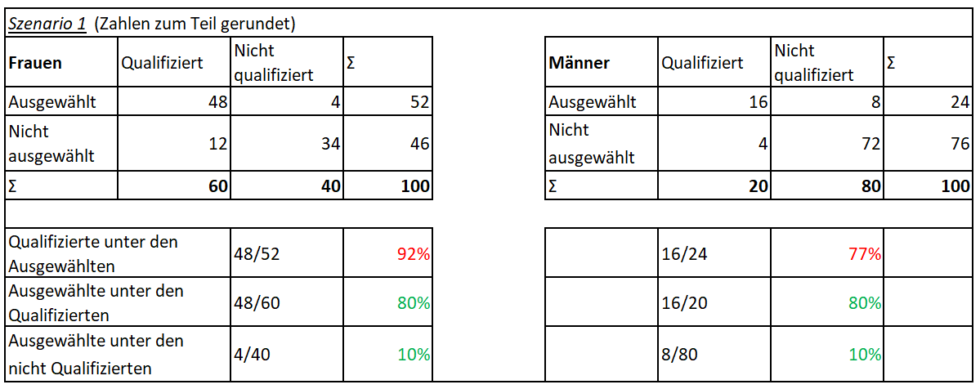
[…] Ein fairer Algorithmus? Szenario 1: Schauen wir uns hierzu einmal ein Beispiel mit Zahlen an (siehe Tabelle 1). Stellen wir uns vor, dass eine Personalerin ein KI-System nutzt, um Bewerbungen auszusortieren, die sie sich nicht anzuschauen braucht. Nehmen wir der Einfachheit halber an, wir haben ein Bewerberfeld aus 100 Frauen und 100 Männern. Von den Frauen sind 60 für die Aufgabe qualifiziert, von den Männern nur 20. Nehmen wir weiterhin an, wir haben einen Algorithmus, der von den 60 qualifizierten Frauen 48 an die Personalerin weiterleitet und von den 20 qualifizierten Männern 16. Außerdem würde er von den 30 [jb: 40] nicht qualifizierten Frauen drei [jb: vier] und von den 80 nicht qualifizierten Männern acht durchwinken. Analysieren wir diesen Algorithmus statistisch, würden wir feststellen, dass er unabhängig vom Geschlecht 80% der qualifizierten Personen korrekt erkennt und fälschlicherweise 10% der unqualifizierten Personen als qualifiziert markiert. In dieser Hinsicht ist der Algorithmus also fair. Schaut man sich dann allerdings die Bewerbungen auf dem Tisch der Personalerin an, wären unter den Männern 33% nicht qualifiziert (8 von 24), von den Frauen hingegen nur ca. 8% (4 von 52). Es bekommen also wesentlich mehr unqualifizierte Männer die Chance auf den Job als unqualifizierte Frauen, sowohl prozentual als auch in absoluten Zahlen.

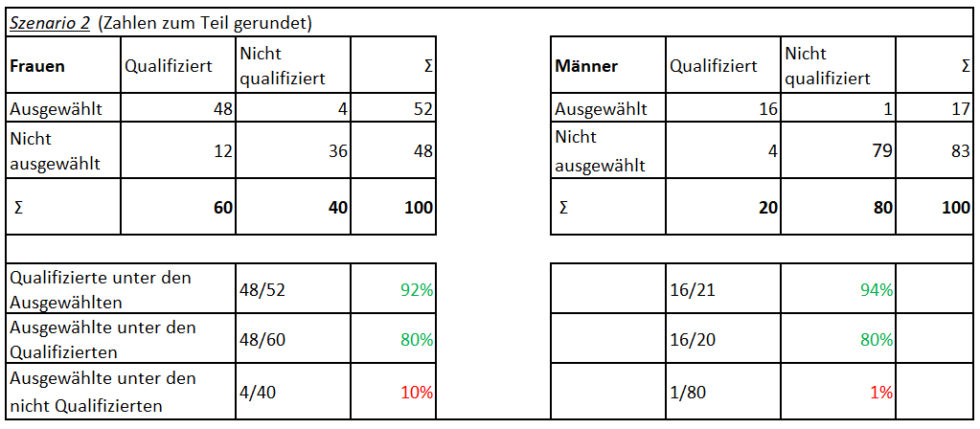
Ein fairer Algorithmus? Szenario 2: Hält man dies für inakzeptabel, könnte man stattdessen ein System trainieren, in dem die Fehlerquote unter den ausgewählten Männern und Frauen jeweils ähnlich ist (siehe Tabelle 2). Eine Möglichkeit wäre hier, ein System zu finden, das bei ansonsten gleichen Zahlen nur einen einzigen unqualifizierten Mann auswählt. Damit würde sich aber zwangsweise auch eine andere Kenngröße verändern: Während auch hier 10% (4 von 40) der unqualifizierten Frauen eingeladen werden, ist es bei den unqualifizierten Männern nur noch etwa 1% (1 von 80). In diesem Szenario wäre also die Chance einer unqualifizierten Frau, dass ihre Bewerbung vom System akzeptiert wird, zehnmal so hoch wie die eines unqualifizierten Mannes. Auch dies kann man für unfair halten. Aufgrund der mathematischen Abhängigkeiten gibt es jedoch keine Möglichkeiten, ein System zu trainieren, das in all diesen Hinsichten ausgeglichen ist.

Welches dieser möglichen Szenarien nun den fairen (oder zumindest faireren) Ansatz darstellt, ist keine mathematische Frage, sondern hängt vom Kontext und von ethischen Überlegungen ab. In unserem Fall kann man es zum Beispiel für wichtig halten, dass die Wahrscheinlichkeit, dass eine unqualifizierte Bewerbung auf dem Tisch der Personalerin landet, für beide Gruppen gleich groß ist. Dann müsste man sich für Szenario 1 entscheiden. Alternativ könnte man aber auch den existierenden Ungleichheiten in unserer Gesellschaft entgegenwirken und daher die Wahrscheinlichkeit minimieren wollen, dass Stellen an nicht qualifizierte Männer gehen. Dies spräche für Szenario 2.

Ende des Auszugs aus dem Originaltext.

Kontextualisierung: Bewerbung als Jockey#

100 Frauen und 100 Männer bewerben sich auf um einen Ausbildungsplatz. Ein anschauliches Beispiel wäre schön: Gibt es Jobs, für die Frauen nicht vorwiegend qua überkommender Tradition oder macht- und durchsetzungsorientierter Sozialisation, sondern qua genetischer Ausstattung geeigneter sind als Männer?

Vielleicht ist Jockey (Wikipedia) so ein Beruf?

„Rennreiter müssen zwischen 52 und 55 Kilogramm wiegen“, sagt Markus Feck, der Fitnesscoach an der Kölner Jockeyschule. http://kurt.digital/2019/07/24/berufswunsch-jockey-zwischen-risiko-und-der-liebe-zum-pferd/

Wenn es darum geht, Menschen zu finden, die mit einem Körpergewicht von max. 55kg ein Höchstmaß an Kraft und Ausdauer erreichen, habe hier Frauen naturgemäß Vorteile – sie sind im Durchschnitt einfach kleiner. Und tatsächlich:

Im Jahr 2017 waren nicht weniger als drei Viertel der Schüler der beiden wichtigsten Ausbildungsstätten für Pferderennen (die British Racing School und das Northern Racing College) weiblich. https://de.wikipedia.org/wiki/Jockey

Training des Modells#

Mit den Daten von vielen Bewerbern trainieren wir einen Klassifikator. Dann testen wir den Klassifikator mit 100 weiblichen und 100 männlichen Bewerbern, von denen wir die Eignung bereits kennen (condition positive): Was sagt die der Klassifikator voraus?

Wir zählen dazu die tatsächlichen und die von der KI vorhergesagten Werte für “Einladen” oder “Ablehnen” in der Gesamtmenge von Bewerbern aus – und zwar getrennt für Frauen und Männer. Wir erhalten zwei Confusion Matritzen:

# CM ... Confusion Matrix für Szenario 1: siehe Originaltext und Tabelle
CM_Szenario1_Frauen  = { "TP": 48, "FP": 4, "TN": 36, "FN": 12 }
CM_Szenario1_Maenner = { "TP": 16, "FP": 8, "TN": 72, "FN":  8 }

besser gendern?

In dem Beispiel geht es um Menschen beiderlei Geschlechts, die sich auf einen Job bewerben. Damit schlüpfen Sie in eine Rolle, nämlich die Rolle des Bewerbers. Solange wir über eine Rolle reden, werden wir das (zwar historisch bedingte und Ungleichheit dokumentierende, nichtsdestrotrotz eingeführte und sprachlich flüssig verwendbare) grammatikalische Genus der verwenden. Alternativen wie “der/die sich Bewerbende” wären umständlicher und schützen auch nicht vor der Verwendung eines grammatischen Genus.

Szenario 1#

Grundlage der folgenden Visualisierung:

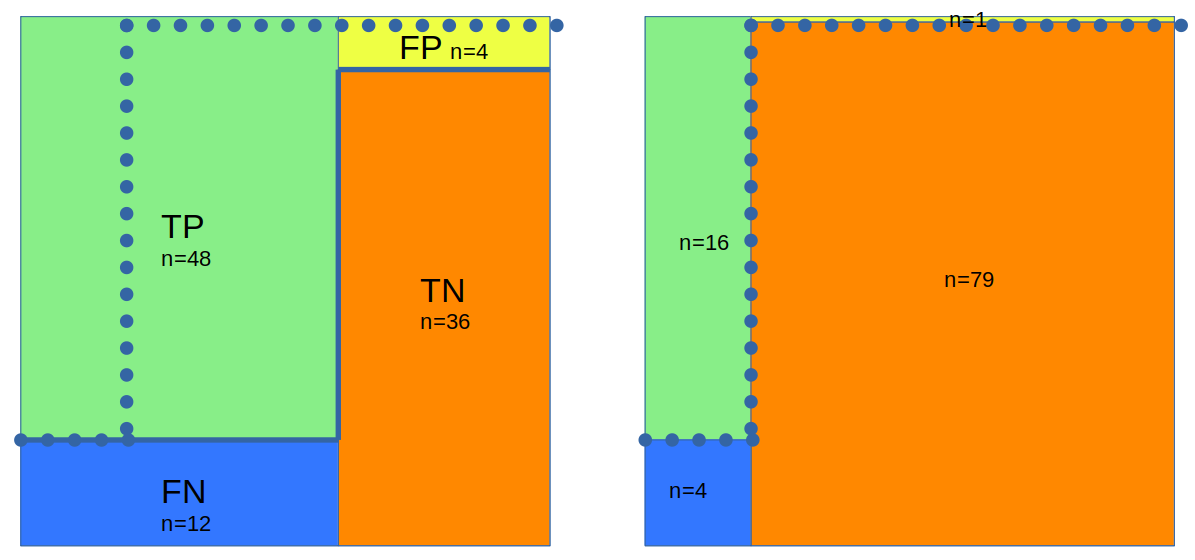
Die Confusion Matrix von Szenario 1 visualisiert als Flächen im Einheitsquadrat (hier: 10 * 10 cm).

Links Gruppe 1 (in unserem Beispiel Frauen), rechts Gruppe 2 (in unserem Beispiel Männer):

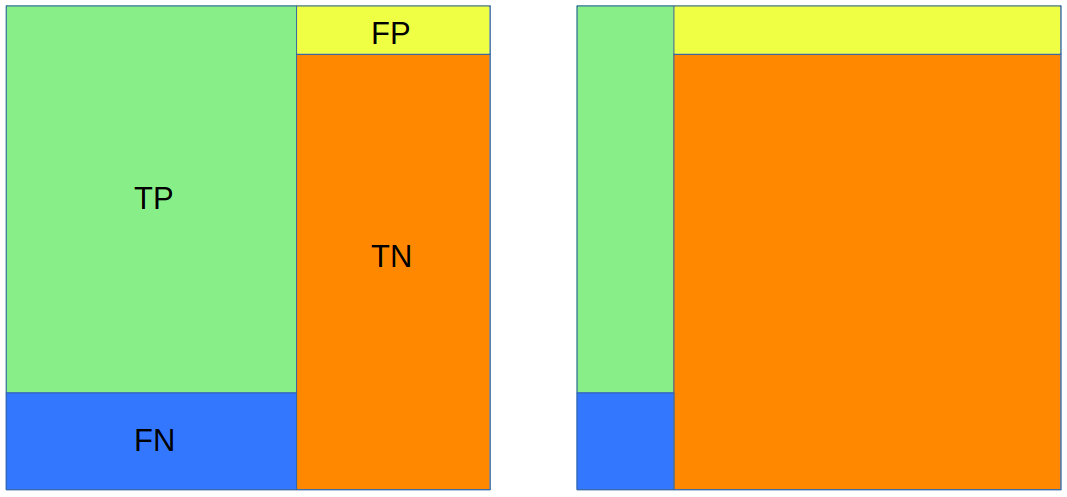
Die Confusion Matrix wird in der Literatur in verschiedenen Orientierungen dargestellt.

Wir verwenden für die Confusion Matrix das Layout “predicted - actual”:

  • Im Einheitsquadrat bilden die tatsächlich positive und negative Gruppe zwei nebeneinanderliegende senkrechte Säulen.

  • TP und FP liegen horizontal nebeneinander.

Dieses Layout wird auch verwendet:

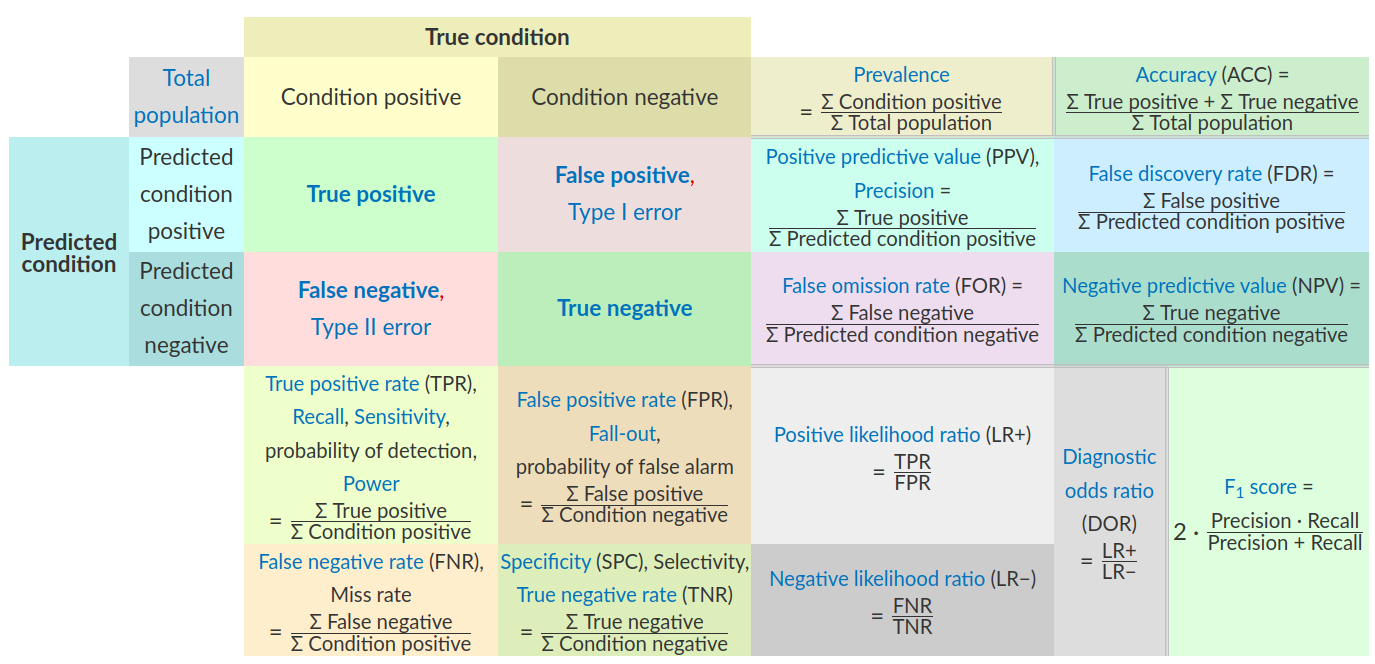
Quelle, mit Links in die entsprechenden Wikpedia-Siten: https://afraenkel.github.io/fairness-book/content/05-parity-measures.html#quantitative-metrics-for-evaluation

VORSICHT Verwechlungsgefahr: In vielen Artikeln der Wikipedia wird die Confusion Matrix typischerweise im Layout “actual - predicted” angelegt (d.h. TP und FP liegen senkrecht untereinander), insbesondere in:

Rechnung Gruppe Frauen, Szenario 1#

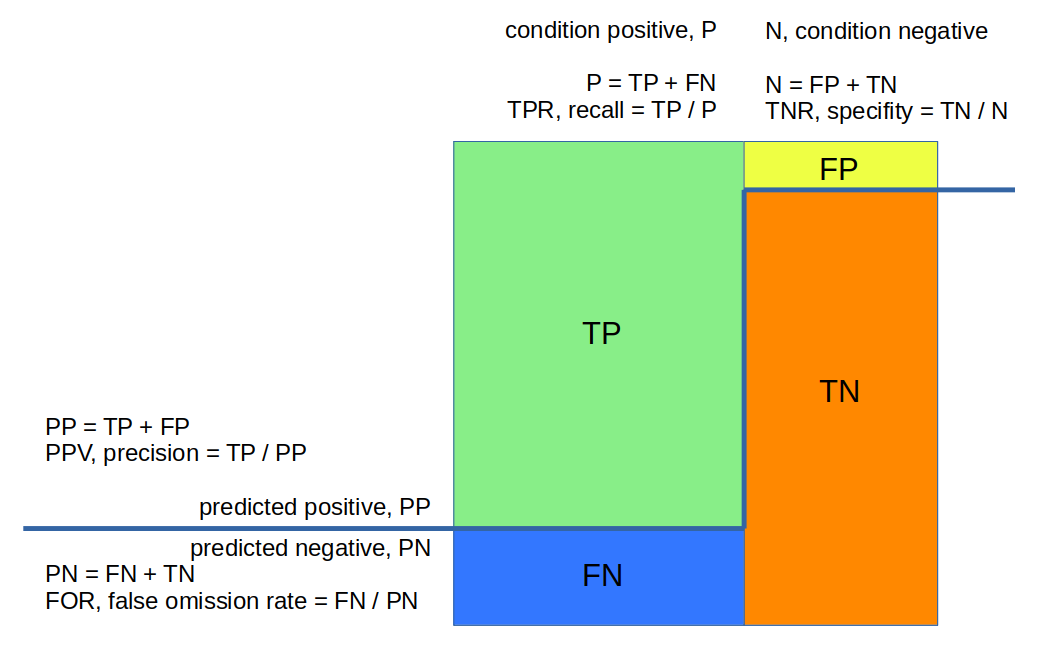
linke Hälfte des Quadrates: Condition Positiv, qualifiert; im grün-blauen Farbspektrum:

  • oben TP = grün (#88ee88)

  • unten FN = blau (#3377ff)

rechte Hälfte des Quadrates: Condition Negativ, nicht qualifiziert, im gelb-rotem Farbspektrum:

  • oben FP = gelb (#eeff44)

  • unten TN = rot (#ff8800)

from myst_nb import glue
CM = CM_Szenario1_Frauen  = { "TP": 48, "FP": 4, "TN": 36, "FN": 12 }
#for k,v in CM.items(): glue(k,v)

P, N#

Von den 100 weiblichen Bewerbern seien P = 60 tatsächlich (“empirisch”, “beobachtbar”) für die Ausbildung qualifiziert ():

P = CM['TP'] + CM['FN']
P_d = "P<br>beobachtet (observed) Positiv:<br>"
glue("P", P)

60

Die restlichen N = 40 sind dagegen nicht qualifiziert ():

N = CM['TN'] + CM['FP']
N_d = "N<br>beobachtet (observed) Negativ:<br>"
glue("N", N)

40

Prävalenz#

Die Prävalenz ist der Anteil der qualifizierten Bewerbern zu allen Bewerbern:

prevalence = P / (P + N)
prevalence_d = "Prävalenz:<br>P / (P + N)<br> = "
glue("prevalence", prevalence)

0.6

identifiziere qualifizierte Bewerber#

Wir betrachten zunächst lediglich die qualifizierten Bewerber:

TP, TPR#

TP, true positive: Unsere KI schafft es, unter den P = 60 qualifizierten Frauen TP = 48 korrekt zu identifizieren:

TP = CM['TP']
TP_d = "TP<br>Treffer:<br>"
glue("TP", TP)

48

TPR, true positive rate, Sensitivität, Recall: das Verhältnis von korrekt als qualifiziert vorhergesagten Bewerbern (TP) zu den tatsächlich qualifizierten (P) Bewerbern ( / ):

TPR = TP / P
TPR_d = "TPR<br>True Positive Rate<br>Sensitivität, Recall:<br>TP / P = "
glue("TPR", TPR)

0.8

A. Schomäcker: “Ausgewählte unter den Qualifizierten: 48/60 = 80%” ist also TPR.

FN, FNR#

FN, false negatives: Auf der Suche nach den qualifizierten Bewerbern werden leider auch einige der tatsächlich geeigneten Bewerber fälschlicherweise abgeleht:

FN = CM['FN']
FN_d = "FN<br>zu unrecht abgelehnt:<br>"
glue("FN",FN)

12

Die FNR, false negative rate ist der Anteil der fälschlicherweise abgelehnten Bewerber aus allen tatsächlich qualifizierten Bewerbern ( / ):

FNR = FN / P
FNR_d = "FNR<br>false negative rate:<br>FN / P = "
glue("FNR",FNR)

0.2

TN, TNR#

TN, true negative: Unter den tatsächlich ungeeigneten Bewerbern erkennt die KI fast alle, konkret: P = 36 ():

TN = CM['TN']
TN_d = "TN<br>korrekte Ablehnung:<br>"
glue("TN",TN)

36

Die TNR, true negative rate, Spezifität ist der Anteil der abgelehnten Bewerber aus allen tatsächlich unqualifizierten Bewerbern ( / ):

TNR = TN / N
TNR_d = "TNR<br>true negative rate,<br>Spezifitiät:<br>TN / N = "
glue("TNR",TNR)

0.9

FP, FPR#

FP, false positive: Leider werden damit aber immer noch einige wenige der tatsächlich ungeeigneten Bewerbern fälschlicherweise als geeignet eingestuft.

FP = CM['FP']
FP_d = "FP<br>falscher Alarm:<br>"
FP

4

Die FPR false positive rate ist der Anteil der – fälschlicherweise – als qualifiziert vorhergesagten Bewerber aus den Bewerbern, die aber tatsächlich nicht qualifiziert sind ( / ):

FPR = FP / N
FPR_d = "FPR<br>false positive rate:<br>FP / N = "
FPR

0.1

Schomäcker: “Ausgewählte unter den nicht Qualifizierten: 4/40 = 10%” ist also FPR.

PP, PPV#

PP, positive predicted: Auf dem Schreibtisch der Personalerin landen also die TP und die FP ():

PP = TP + FP
PP_d = "PP<br>vom Test ausgewählt,<br>predicted positive:<br>"
PP

52

Die PPV, predicted positive rate, precision ist das Verhältnis von korrekt als qualifiziert vorhergesagten Bewerbern (TP (icons/TP.png)) zu den allen als qualifiziert vorhergesagten (PP) Bewerbern ( / ):

PPV = TP / PP
PPV_d = "PPV<br>Positive predictive value,<br>precision:<br>TP / PP = "
PPV = round(PPV, 3)
PPV

0.923

Der Unterschied zwischen TPR und PPV ist also die Grundgesamtheit:

  • TPR bezieht die TP auf eine tatsächliche beobachtbare Menge

  • PPV bezieht zwei vorhergesagte Werte aufeinander

Schomäcker: “Qualifizierte unter den Ausgewählten: 48/52 = 92%” ist also PPV.

Leider leider …#

PN, negative predicted: Gar nicht erst in die engere Wahl kommen alle zurecht oder fälschlicherweise mit Negativ vorhergesagten Bewerber ():

PN = TN + FN
# oder auch einfach der Rest: PN = 100 - PP
PN_d = "PN<br>vom Test abgelehnt,<br>predicted negative:<br>"
PN

48

Die FOR, false omission rate gibt an, wie viele der abgelehnten Bewerber fälschlicherweise abgelehnt wurden ( / )::

FOR = FN / PN
FOR_d = "FOR<br>false omission rate:<br>FN / PN = "
FOR

0.25

Confusion Matrix predicted - actual#

print(f"""Frauen\t{P=}\t{N=}
{PP=}\t{TP=}\t{FP=}\t{PPV=}
{PN=}\t{FN=}\t{TN=}\t{FOR=}
\t{FNR=}\t{TNR=}
""")

Frauen	P=60	N=40
PP=52	TP=48	FP=4	PPV=0.923
PN=48	FN=12	TN=36	FOR=0.25
	FNR=0.2	TNR=0.9

Wenn wir diese Rechnung ebenfalls für Männer durchführen, erhalten wir zwar für TPR und FPR die gleichen Werte:

Analysieren wir diesen Algorithmus statistisch, würden wir feststellen, dass er unabhängig vom Geschlecht 80% der qualifizierten Personen korrekt erkennt und fälschlicherweise 10% der unqualifizierten Personen als qualifiziert markiert. In dieser Hinsicht ist der Algorithmus also fair. (Schomäcker)

  • TPR, “Ausgewählte unter den Qualifizierten”:

    • Frauen: 48 / 60 = 80%

    • Männer: 16 / 20 = 80%

  • FPR, “Ausgewählte unter den nicht Qualifizierten”:

    • Frauen: 4 / 40 = 10%

    • Männer: 8 / 80 = 10%

Equalized odds [ … is satified ] if the subjects in the protected and unprotected groups have equal true positive rate and equal false positive rate https://en.wikipedia.org/wiki/Equalized_odds

Das Fairnessmaß equalized odds ist also erfüllt.

Aber für PPV unterscheiden sich die Werte stark:

Schaut man sich dann allerdings die Bewerbungen auf dem Tisch der Personalerin an, wären unter den Männern 33% nicht qualifiziert (8 von 24), von den Frauen hingegen nur ca. 8% (4 von 52). (Schomäcker)

  • PPV, “Qualifizierte unter den Ausgewählten”:

    • Frauen: 48 / 52 = 92%

    • Männer: 16 / 24 = 66%

Predictive parity [ … is satified ] if the subjects in the protected and unprotected groups have equal PPV. https://en.wikipedia.org/wiki/Fairness_(machine_learning)

Das Fairnessmaß predictive parity ist also verletzt.

Es bekommen also wesentlich mehr unqualifizierte Männer die Chance auf den Job als unqualifizierte Frauen, sowohl prozentual als auch in absoluten Zahlen. (Schomäcke)

Korrekt.

Zu diskutieren: Wie bewertet man dies? Von welchen Rahmenbedingungen, normativen Vorstellungen, politischen Positionen hängt es ab, wie man das bewertet – und wodurch entsteht jeweils der Zusammenhang?

Szenario 2#

[Man könnte] stattdessen ein System trainieren, in dem die Fehlerquote [JB: PPV, “Qualifizierte unter den Ausgewählten”] unter den ausgewählten Männern und Frauen jeweils ähnlich ist (siehe Tabelle 2). Eine Möglichkeit wäre hier, ein System zu finden, das bei ansonsten gleichen Zahlen nur einen einzigen unqualifizierten Mann auswählt. Damit würde sich aber zwangsweise auch eine andere Kenngröße verändern: Während auch hier 10% (4 von 40) der unqualifizierten Frauen eingeladen werden, ist es bei den unqualifizierten Männern nur noch etwa 1% (1 von 80).